ベルヌーイの定理

　図1に示すように、側面に小さな穴が空いた水槽を考えます。点1は、大気圧$p_{0}、速度v_{1}、高さz_{1}$の水面上にあり、側面の小さな点2の穴からは、大気圧$p_{0}、速度v_{2}、高さz_{2}$で水が流出しています。

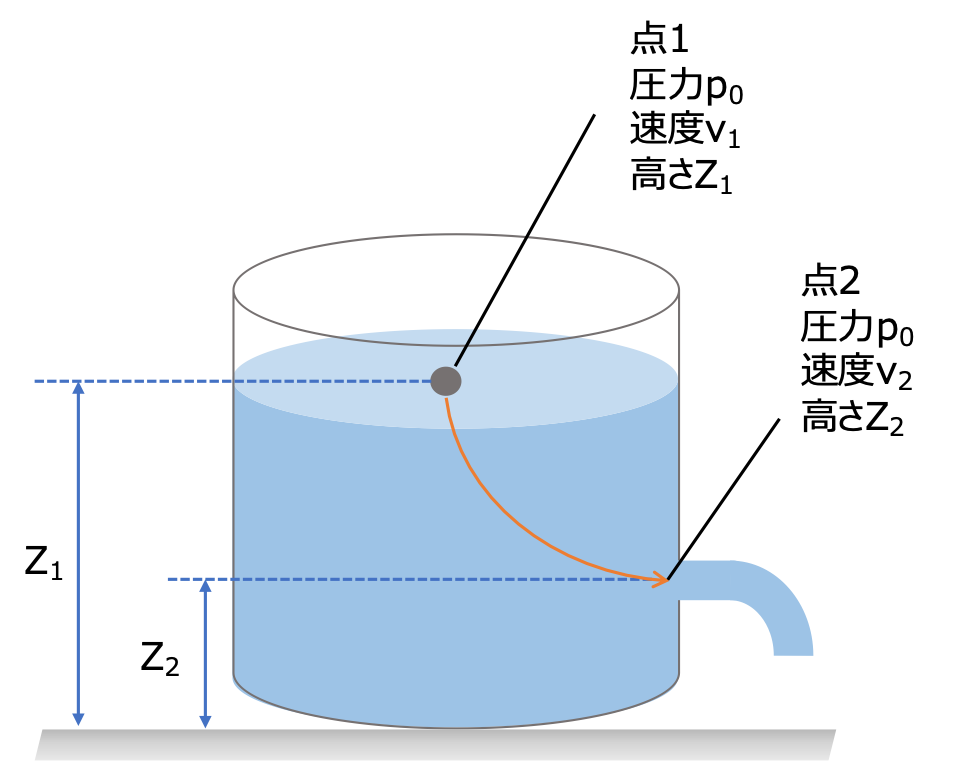
図1　水槽から流れ出る水

　この時の点1と点2の圧力、速度、高さの関係は、式(1)で示すベルヌーイの定理で説明され、「圧力のエネルギー」＋「運動のエネルギー」＋「位置のエネルギー」は一定となります。

$$ p + \frac{1}{2}\rho v^{2} + \rho g z = 一定 　\tag{1} $$

　$p$ は圧力（$P a$）、$\rho$は流体の密度（$kg / m^{3}$）、$v$は流体の速度（$m/s$）、$g$は重力加速度（$m/s^{2}$）、$z$ は高さ（$ m $）です。それぞれの項の単位は下記に示す様に圧力の単位になります。

$\rho v^{2}$ の単位は、$kg / m^{3} \times m^{2}/s^{2} = kg \times m/s^{2} \div m^{2} = N / m^{2} = P a$

$\rho g z$の単位は、$kg / m^{3} \times m/s^{2} \times m = kg \times m/s^{2} \div m^{2} = N / m^{2} = P a$

　式(1)では、圧力が一定であることを示しているだけなのに、何故エネルギーとなるのか？と疑問に思うかもしれません。

　これは、単位体積当たりで考えれば良く、単純に圧力の単位$N / m^{2}$を変形させ、$N \times m / m^{3} = J/ m^{3}$とすると、単位体積($m^{3}$)当たりのエネルギー($J$)の形となります。

　点1と点2の関係はベルヌーイの定理から、式(2)のようになります。

$$ p_{0} + \frac{1}{2}\rho v_{1}^{2} + \rho g z_{1} = p_{0} + \frac{1}{2}\rho v_{2}^{2} + \rho g z_{2} \tag{2}$$

　この時の運動エネルギーを動圧、圧力を静圧といい、これらの和を全圧あるいは総圧と言います。点1の水面の低下速度$v_{1}$は$v_{2}$に比較して十分小さく0とすると、上記の関係は、式(3)のように整理できます。

$$\rho g z_{1} = \frac{1}{2}\rho v_{2}^{2} + \rho g z_{2} \tag{3} $$　

　つまり、点1と点2の静圧は大気圧で同じため、点1の位置エネルギーが点2の動圧と位置エネルギーに変換されたということです。

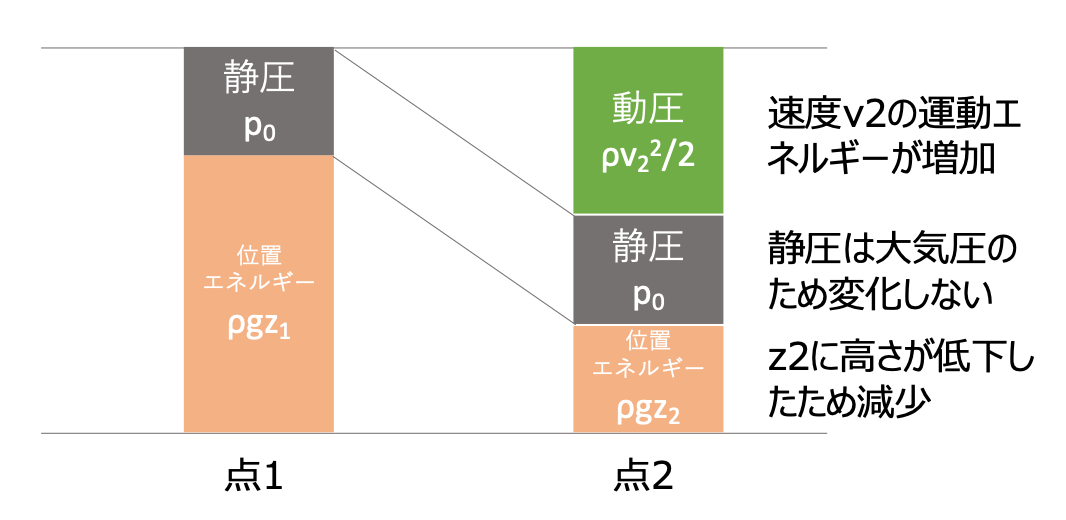
図 2　点１と点２のエネルギーの関係

　式(3)より、$v_{2}$は式(4)の様に変形でき、流出している水の速度を求めることができます。

$$ v_{2} = \sqrt{2 g (z_{1} - z_{2})} \tag{4}$$

　なお、式(1)は式(5)(単位は$ m $)の様に変形でき、それぞれの項は圧力ヘッド、速度ヘッド、位置ヘッドといいます。

$$ \frac{p}{\rho g} + \frac{v^{2}}{2g} + z = 一定 \tag{5} $$

　圧力エネルギー、運動エネルギー、位置エネルギーを全て高さに変換して考えることができ、ポンプの選定でよく登場します。ポンプについては、別途まとめて紹介しようと思います。